티스토리 뷰
EM for GMM
Graphical Model for GMM을 통해 명시적으로 잠재변수 z를 도입하여 graphical model로 모델링하였다.
이제 이 graphical model에서 P(x,z) 결합확률 분포를 구할 수 있고 이를 marginalization해서 x에 대한 주변 확률 분포를 구할 수 있다. 이 페이지에서는 이 P(x)를 maximization 시키는 매개변수를 찾는 것이 목표이다. 하지만 미분을 통한 MLE 방법은 확률변수 z가 잠재되어 있어서 사용할 수 없고, EM 알고리즘을 사용해야 한다.
먼저 GMM을 이용한 classification은 주어진 데이터 x에 대해 이 데이터가 어떠한 Gaussian distribution에서 생성되었는지를 찾는 것이다. reponsibility를 아래와 같이 계산하고 가장 확률값이 높은 k번 째 Gaussian distribution을 해당 데이터의 cluster로 선정하는 것이다.

Expectation Step
이 과정을 expectation step이라고 한다. (reposibility를 사후확률로 이해할 수 있다. )
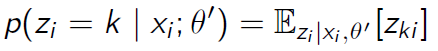
Maximization Step
expectation step에서 계산한 responsibility 값을 이용하여 파라미터를 추정한다. (위에서 계산한 사후확률을 사전확률로써 사용해서 계속 E step, M step을 반복한다. )






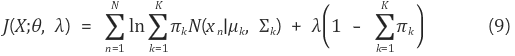




'기계학습' 카테고리의 다른 글
| Graphical Model for GMM (0) | 2019.10.22 |
|---|---|
| Gaussian Mixture Model (GMM) (0) | 2019.10.22 |
| Multinomial Distribution (0) | 2019.10.21 |
| MLE (최대우도추정) (0) | 2019.10.21 |
| Belief Propagation (0) | 2019.10.18 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- gaussian mixture model
- graphical model for GMM
- 상호정보량
- batch normalization
- eigen decomposition
- inference
- 해석가능한 인공지능
- 내적
- Belief Propagation
- jensen's inequality
- convex
- 외적
- conditional independence
- graphical model
- 벡터 미분
- local structure
- posterior
- KL-divergence
- 행렬 미분
- perceptron
- Bayesian Network
- Multinomial Distribution
- EM algorithm
- Absorption
- Statistically Significant
- 조건부 확률
- 특이값 분해
- 작업중..
- Potential function
- 베이즈 정리
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
글 보관함
